Ce casse-tête triangulaire va vous surprendre : saurez-vous tous les repérer ?
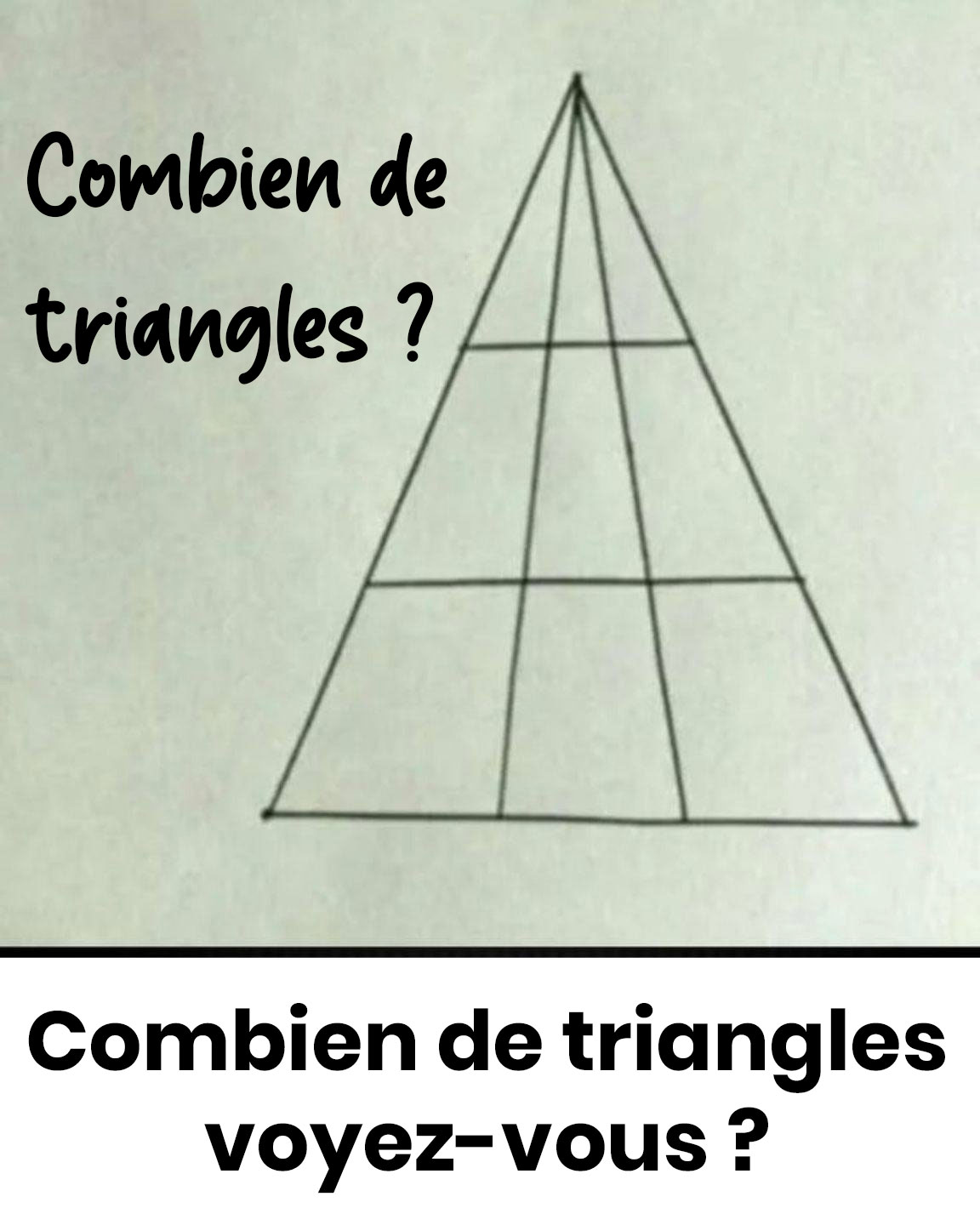
Ce puzzle géométrique semble simple au premier abord, mais il réserve une belle surprise. Derrière cette apparence basique se cachent bien plus de formes que votre œil ne le perçoit initialement. Préparez-vous à découvrir la solution qui étonne même les plus perspicaces.
Le défi des formes dissimulées
Notre perception visuelle a tendance à identifier les triangles les plus apparents tout en négligeant ceux qui se créent par l’assemblage de plusieurs sections. Conséquence : nous tombons souvent dans le piège de la sous-estimation. Dans cette configuration traditionnelle (4 niveaux créés par 3 traits parallèles au côté inférieur), la solution exacte s’élève à 27.
Si vous avez obtenu 26, vous avez vraisemblablement manqué l’un des grands triangles composites – généralement une forme orientée vers le haut s’étendant sur 3 étages, ou un triangle de taille intermédiaire situé sur un côté.
La technique de comptage infaillible

Identifiez méthodiquement les triangles « orientés vers le haut » en fonction de leur dimension :
- Dimension sur 1 niveau : 10
- Dimension sur 2 niveaux : 6
- Dimension sur 3 niveaux : 3
- Dimension sur 4 niveaux : 1
Total partiel pour les triangles « vers le haut » : 10 + 6 + 3 + 1 = 20.
Incorporez ensuite les triangles « orientés vers le bas » générés par l’entrecroisement des lignes : 7.
Résultat final : 20 + 7 = 27.
Petite astuce mémorielle : retenez « 20 pour le haut, 7 pour le bas » et vous échapperez à l’erreur fréquente.
L’approche mathématique simplifiée

Vous préférez une méthode rapide et élégante ? Pour une figure triangulaire principale divisée en n rangées par des segments parallèles à la base (ici n = 4), cette équation donne la réponse :
T(n) = n × (n + 2) × (2n + 1) ÷ 8
Avec n = 4 :
T = 4 × 6 × 9 ÷ 8 = 27
Ce chiffre concorde parfaitement avec notre dénombrement manuel. L’avantage de cette formule, c’est qu’elle intègre automatiquement toutes les configurations possibles, y compris les combinaisons multi-niveaux. Parfait pour confirmer son intuition… ou pour impressionner lors d’une discussion animée !
Pièges courants (et comment les contourner)
- Compter « par étages » sans considérer les grandes formes traversant plusieurs niveaux : l’oubli typique concerne souvent un triangle de 3 niveaux.
- Négliger les triangles inversés (« vers le bas ») : moins évidents visuellement, ils comptent pourtant pour 7 unités.
- Imaginer des lignes verticales supplémentaires : certaines versions de ce défi incluent effectivement des verticales, ce qui change le total (mais jamais vers 26). Vérifiez toujours la configuration précise avant de valider.
- Compter deux fois certaines formes : adoptez une progression méthodique par taille pour éviter les répétitions.
Pour approfondir le défi
- Modifiez le nombre de rangées : expérimentez la formule avec n = 3 ou n = 5 et confrontez avec un comptage visuel – excellent exercice d’observation.
- Jouez contre la montre : accordez-vous 60 secondes pour atteindre 27. La clé ? Dénombrez d’abord les « vers le haut », puis ajoutez les « vers le bas ».
- Transmettez l’astuce : partager une méthode, c’est l’ancrer durablement dans sa mémoire (et s’assurer de briller lors des prochains défis entre amis).
Derrière cette apparente simplicité géométrique se cache une véritable leçon de logique visuelle… et la satisfaction délicieuse de maîtriser un casse-tête qui défie les apparences !









